A Closer Look: Concepts to Ponder on

In tackling complex tasks, it is always important to look back on the fundamental principles behind them. With the fourth challenge of the International Robotics Championship: A Friend in Need, is a friend indeed, worry not! Let us investigate further on the scientific concepts that can help better understand the task– it might just hold the key to solving it!

Law of the Lever

A lever is one of the simple machines that has laid a foundation on engineering. It consists of two basic components: a beam fixed at a point called the fulcrum. The lever rotates on a point on itself, providing what we call leverage.

The Law of the Lever can be interpreted as such:

“As the lever rotates around the fulcrum, points farther from this pivot move faster than points closer to the pivot. Therefore, a force applied to a point farther from the pivot must be less than the force located at a point closer in, because power is the product of force and velocity (Uicker, Pennock and Shigley, 2010).”

Meaning to say, given two points a and b where a has a greater distance from the fulcrum, the input force applied in point a would be amplified, thereby increasing the output force expedited in point b. If the reverse was true, and the distance between the point of input force (point a) is shorter than the point of output force (point b), then the lever reduces the magnitude of the force.

For key takeaways, the further from the fulcrum a force is applied, then the less effort is needed to move the lever. 

Rotation Angle

When objects rotate about some axis—for example, when the compact disc rotates about its center—each point in the object follows a circular arc. Consider a line from the center of the CD to its edge. Each pit used to record sound along this line moves through the same angle in the same amount of time. The rotation angle is the amount of rotation and is analogous to linear distance. We define the rotation angle Δθ to be the ratio of the arc length to the radius of curvature:      

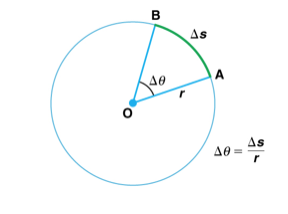
The arc length Δs is the distance traveled along a circular path. Note that r is the radius of curvature of the circular path.

We know that for one complete revolution, the arc length is the circumference of a circle of radius r. The circumference of a circle is 2πr. Thus for one complete revolution, the rotation angle is

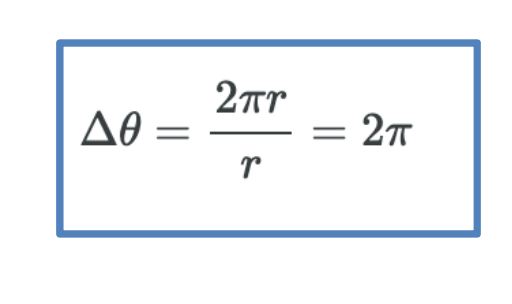
The result is the basis for defining the units used to measure rotation angles, Δθ to be radians (rad), defined so that 2π rad = 1 revolution.

Angular Velocity

How fast is an object rotating? We define angular velocity ω as the rate of change of an angle. In symbols, this is 

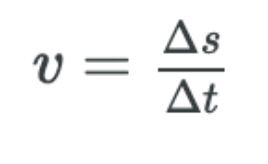
where an angular rotation Δθ takes place in a time Δt. The greater the rotation angle in a given amount of time, the greater the angular velocity. The units for angular velocity are radians per second (rad/s).

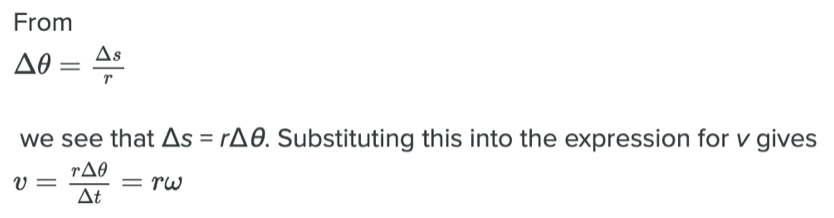
Angular velocity ω is analogous to linear velocity v. To get the precise relationship between angular and linear velocity, we again consider a pit on the rotating CD. This pit moves an arc length in a time.

Rotational Inertia

Rotational inertia is the property of an object to counter the direction of its spin in relation to a rotational axis. This is a fundamental concept in physics that is used in problems involving angular momentum and how the distribution of mass correlates to the rotational motion or velocity of a spinning object. 

Rotational inertia is dependent on (1) the mass and (2) the distribution of the mass relative to the axis of rotation. Moreover, it is also important to account the momentum of the object. A mass that moves farther from the center or point of rotation is harder to change rotational velocity than a mass that is closer to the axis of rotation.

In essence, the heavier the mass of the rotating object, the harder it is to change the rotational velocity and direction of its spin. Keep in mind these handy lessens as they can help you better understand the concepts behind the challenge. We hope this helps, and good luck to all IRC participants! 

References:

– Uicker, John; Pennock, Gordon; Shigley, Joseph (2010). Theory of Machines and Mechanisms (4th ed.). Oxford University Press, USA. ISBN 978-0-19-537123-9.

– Lumen Learning , Physics